Come creare una cupola geodetica in stile Temcor in Autodesk Inventor: 8 passaggi

2024 Autore: John Day | [email protected]. Ultima modifica: 2024-01-30 10:04

Questo tutorial ti mostrerà come creare una cupola in stile Temcor usando solo un po' di matematica.

La maggior parte delle informazioni in questo tutorial sono state raccolte dall'ingegneria inversa di TaffGoch del metodo di suddivisione della vecchia stazione del Polo Sud Amundsen-Scott, quindi un enorme grazie a lui!

Uno dei principali vantaggi delle cupole Temcor è il loro basso numero di puntoni unico: aumenta aritmeticamente con la frequenza, non diversamente dalla normale griglia geodetica triacontaedrica di Duncan Stuart (metodo 3*), ma il risultato sembra molto più piacevole.

Per semplicità, la frequenza della cupola che stiamo realizzando è 14, quindi i fattori di accordo possono essere confrontati con il modello Temcor di TaffGoch.

Il file.ipt di Inventor 2016 è incluso alla fine dell'esercitazione.

*AGGIORNARE*

Ho descritto il Metodo 4 come la normale griglia geodetica triacontaedrica di Duncan Stuart, ma non lo è. Il metodo è stato in realtà inventato da Christopher Kitrick, che nel suo articolo del 1985, "Geodesic Domes", ne descrisse la costruzione. Inoltre, nel suo articolo del 1990, "A Unified Approach to Class I, II & III Geodesic Domes", delinea altri 8 metodi, uno dei quali è il Metodo 3 di Duncan Stuart, l'altro il suo "Metodo 4" e, sorprendentemente abbastanza, un metodo analogo a quello di Temcor, che chiama "Metodo aa" (il passaggio 7 mostra come Temcor ha modificato "Metodo aa"). In un futuro istruibile, descriverò la costruzione dei metodi delineati in quest'ultimo documento.

Passaggio 1: parametri utente

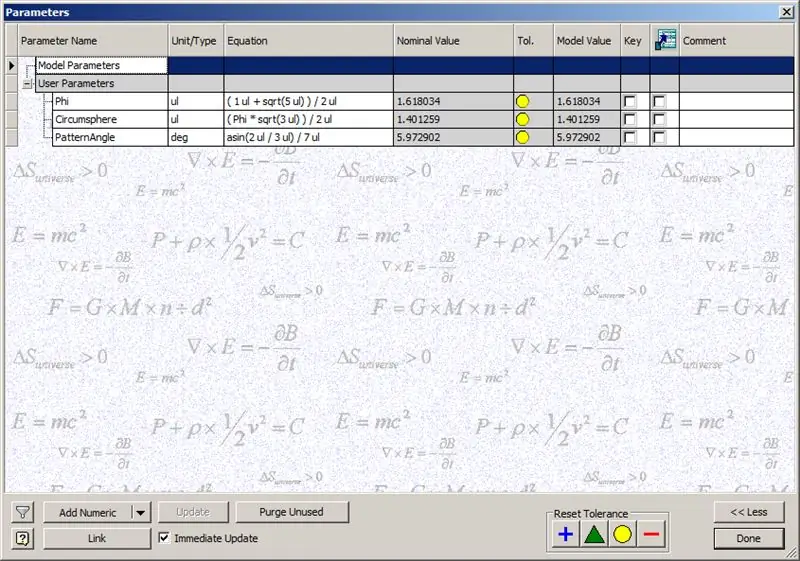
Prima di iniziare a costruire la cupola, inserire i parametri mostrati:

Phi - La Sezione Aurea. Definito come ((1+√5/)2

Circumsphere - Questa è la circumsfera di un dodecaedro, definita come ((Phi*√3)/2)

PatternAngle - Questo è l'angolo centrale di un dodecaedro. Poiché la frequenza della nostra cupola è 14, dividiamo questo angolo centrale per metà della frequenza, in questo caso 7.

Passaggio 2: disegnare un rettangolo dorato

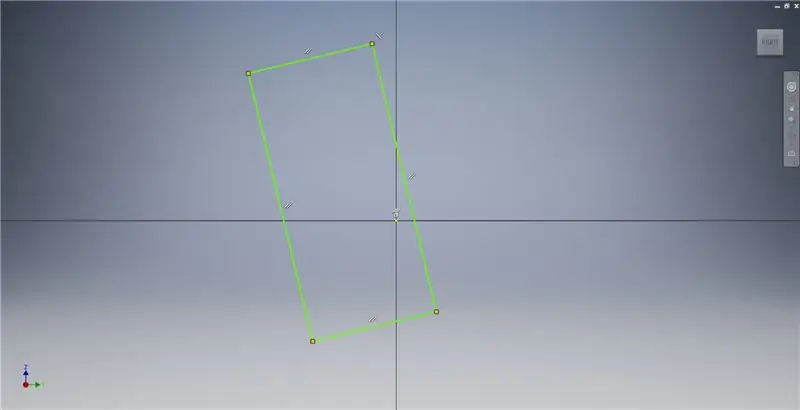
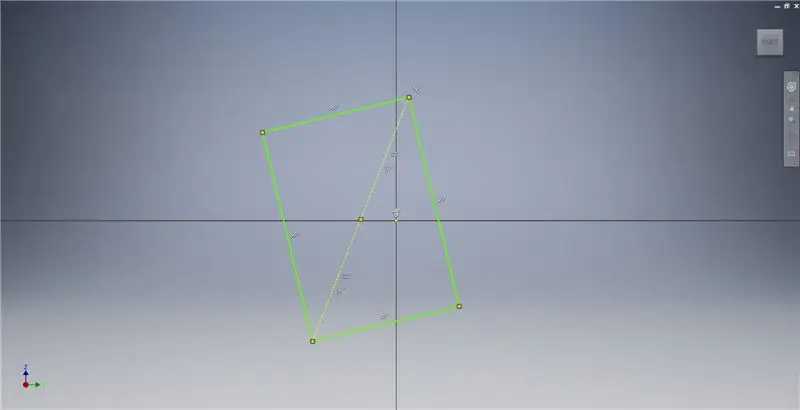
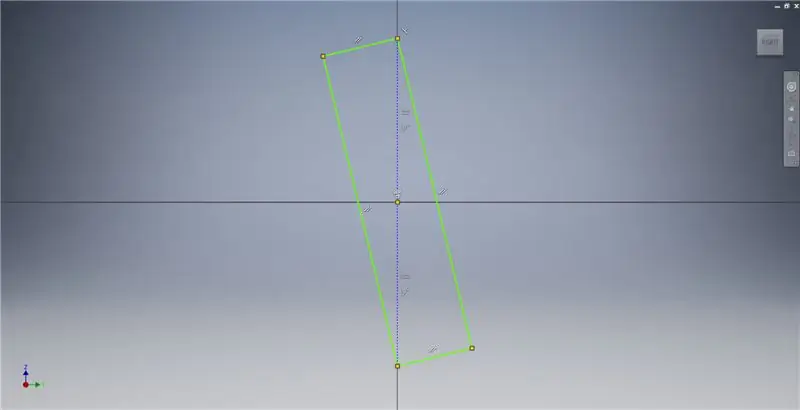
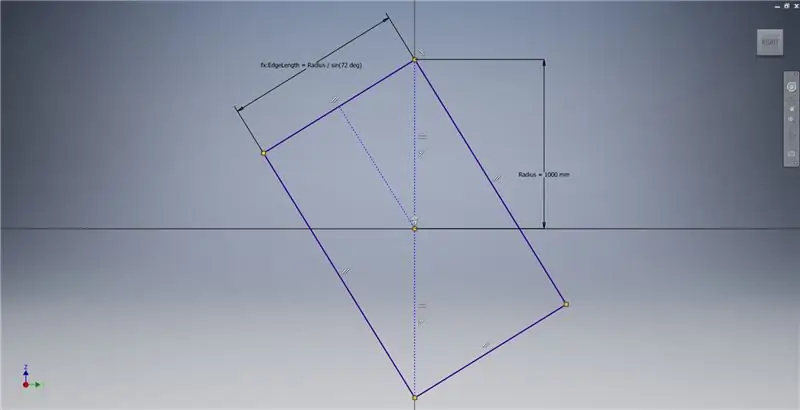
Inizia uno schizzo sul piano YZ, quindi crea un rettangolo a tre punti come mostrato, facendo riferimento alle note dell'immagine per ulteriori informazioni che descrivono la creazione di un rettangolo dorato.

Passaggio 3: creazione di un rettangolo dorato²

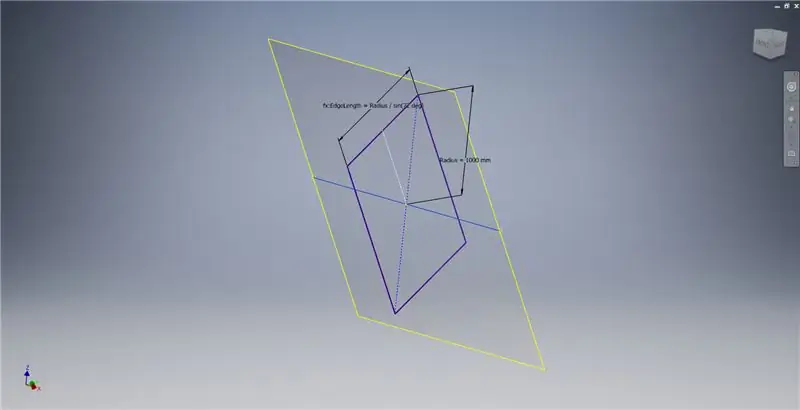
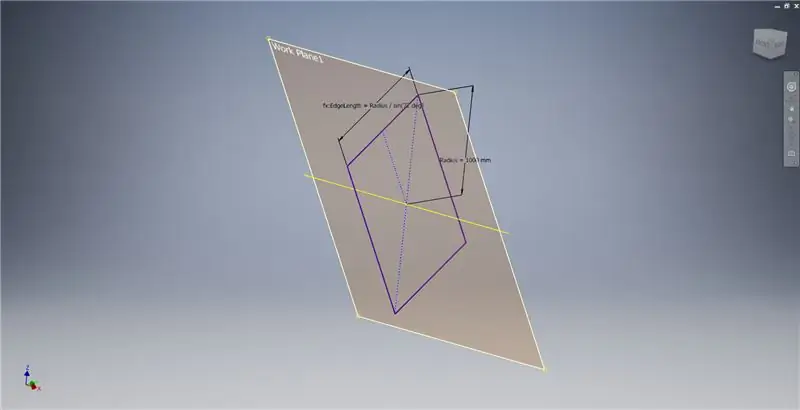
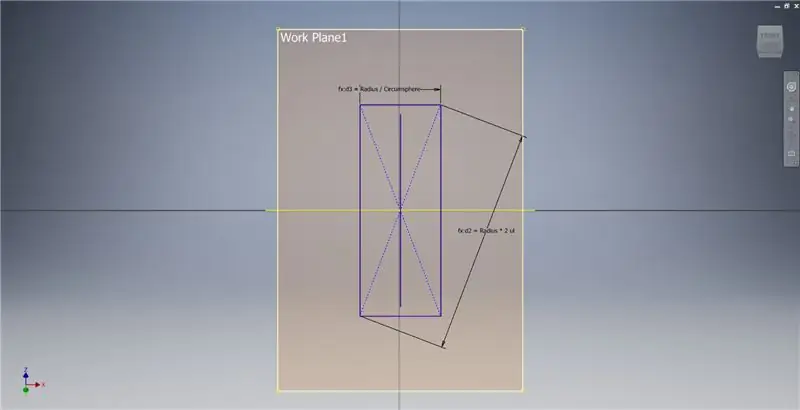
Crea un piano di lavoro utilizzando l'asse X e la linea evidenziata nella prima immagine, quindi inizia un altro schizzo su questo piano di lavoro. Costruisci un rettangolo con punto centrale partendo dall'origine, quindi quota il rettangolo come mostrato nella terza immagine.

Passaggio 4: creazione del triangolo Triacon 2v

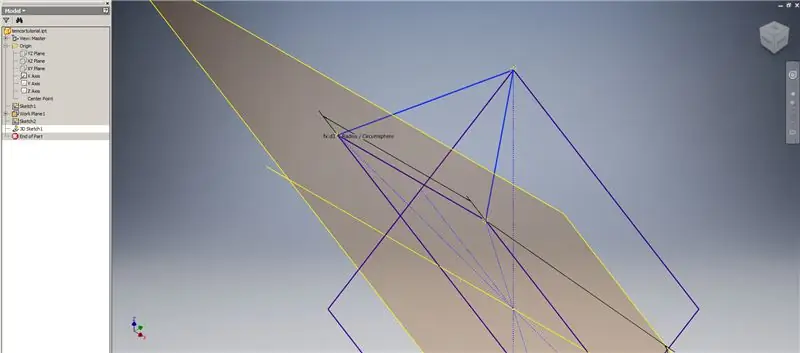
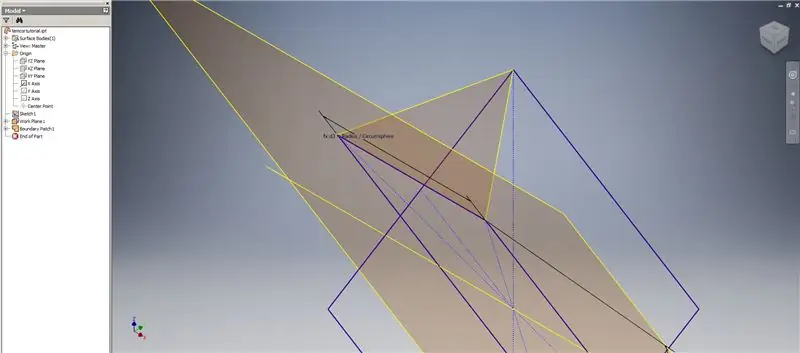
Ora che abbiamo tutta la geometria di cui abbiamo bisogno, forma la zona di confine nella seconda immagine usando il metodo che preferisci. Ho scelto di fare uno schizzo 3D, ma lo schizzo su un altro piano di lavoro avrebbe funzionato altrettanto bene.

Passaggio 5: creazione dei piani di intersezione

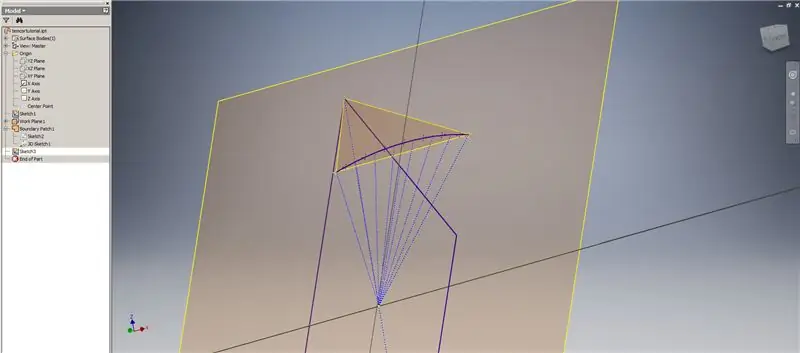
Inizia un altro schizzo sul primo piano di lavoro ("Work Plane 1") che hai creato, proietta gli angoli del Rettangolo Aureo², quindi collega questi punti e l'origine per formare l'angolo centrale del triacontaedro 2v. Dividilo per metà della frequenza della cupola, come se stessi iniziando un guasto del Metodo 2. Posiziona i punti sui punti medi degli accordi.

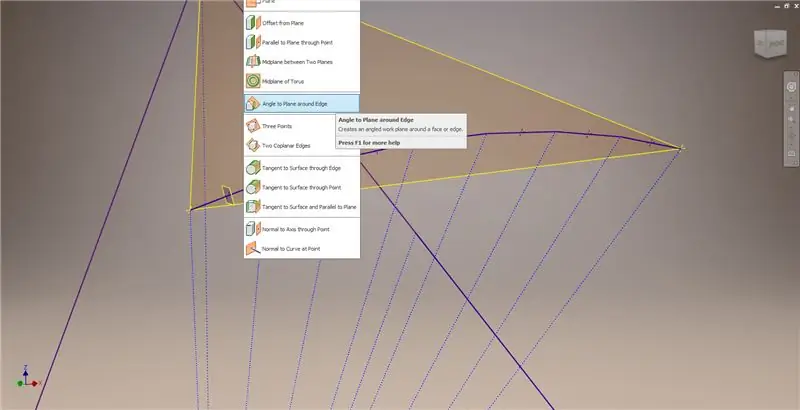
Esci dallo schizzo, quindi crea un piano usando una delle corde e il suo punto medio, come mostrato nella seconda immagine. Quindi, crea un altro piano di lavoro usando "Angolo al piano intorno al bordo". Seleziona Piano di lavoro 1 e una delle linee di costruzione mostrate nell'immagine al centro a destra e in basso a sinistra. Accetta l'angolo predefinito di 90 gradi, altrimenti il resto della suddivisione non sarebbe corretto. Ripeti il processo usando il resto degli accordi e delle linee di costruzione per ottenere il risultato nell'immagine in basso a destra.

Passaggio 6: creazione delle curve di intersezione e formazione della suddivisione

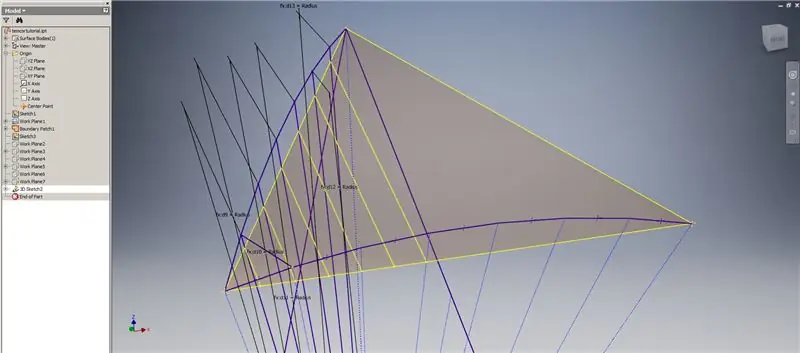
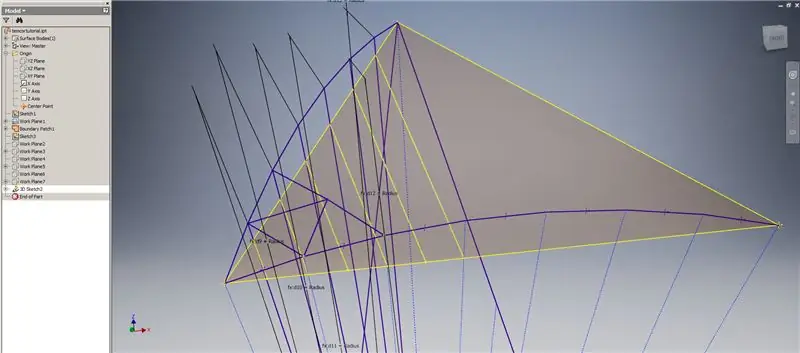
Inizia uno schizzo 3D, quindi crea curve di intersezione utilizzando i piani di lavoro appena creati e la patch di confine, formando le linee mostrate nell'immagine in alto.

Disegna linee coincidenti con i punti finali delle curve di intersezione come mostrato nell'immagine 2. Rendile tutte uguali al raggio della cupola. Disegna le corde che uniscono le linee che giacciono sulle curve di intersezione. Collega qualsiasi geometria che appaia abbastanza vicina da formare un triangolo della suddivisione. Fare riferimento alle prossime 10 immagini per quali accordi rispecchiare sui piani di lavoro dell'intersezione: possono spiegarlo meglio di semplici parole.

Passaggio 7: completamento della cupola

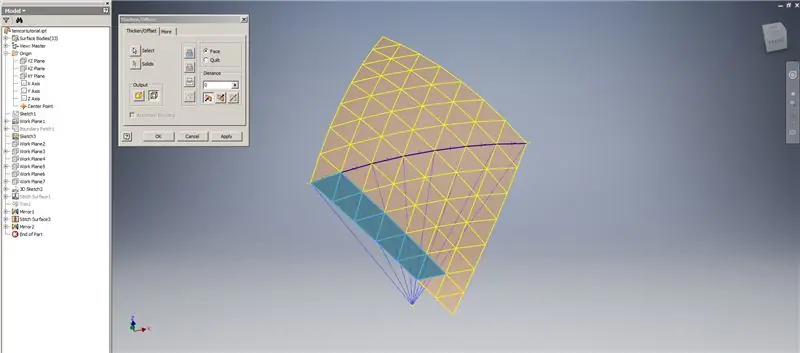
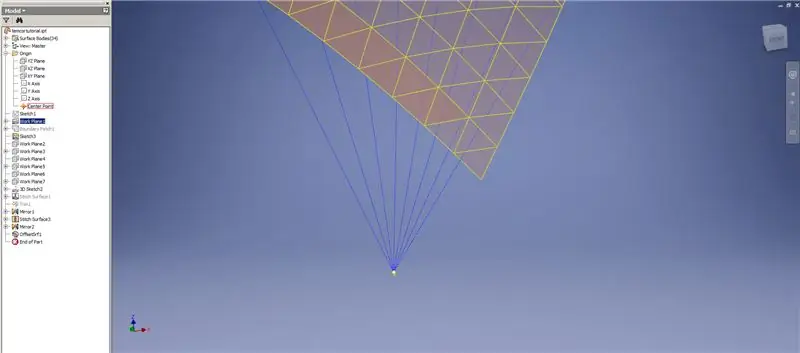
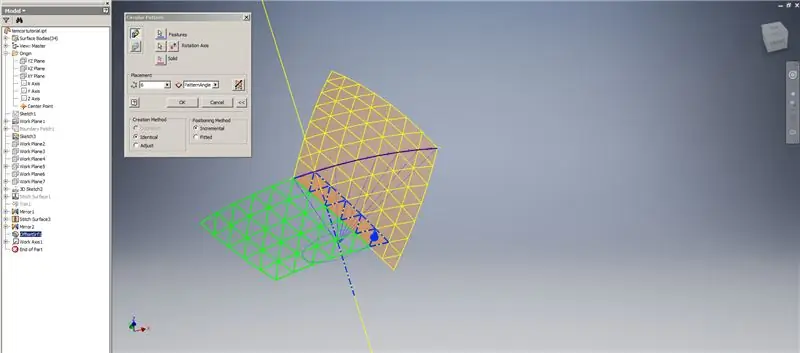
Crea un addensare/offset delle righe inferiori, omettendo le ultime due righe di triangoli. Modella il nuovo OffsetSrf 6 volte o ((Frequency=14)/2)-1. Nascondi OffsetSrf, cuci le superfici modellate, quindi specchia la superficie cucita con il piano YZ. Crea piani di lavoro appoggiati sui vertici del triangolo superiore, come mostrato nell'immagine 6. Taglia le superfici cucite e specchiate usando questi nuovi piani di lavoro, quindi unisci le superfici rimanenti. Modella quest'ultima superficie lungo l'asse Z, quindi cuci insieme queste superfici finali e il gioco è fatto!

Passaggio 8: controllo degli accordi

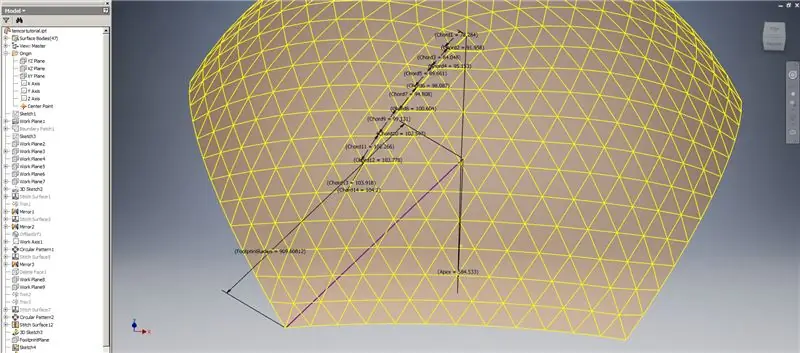
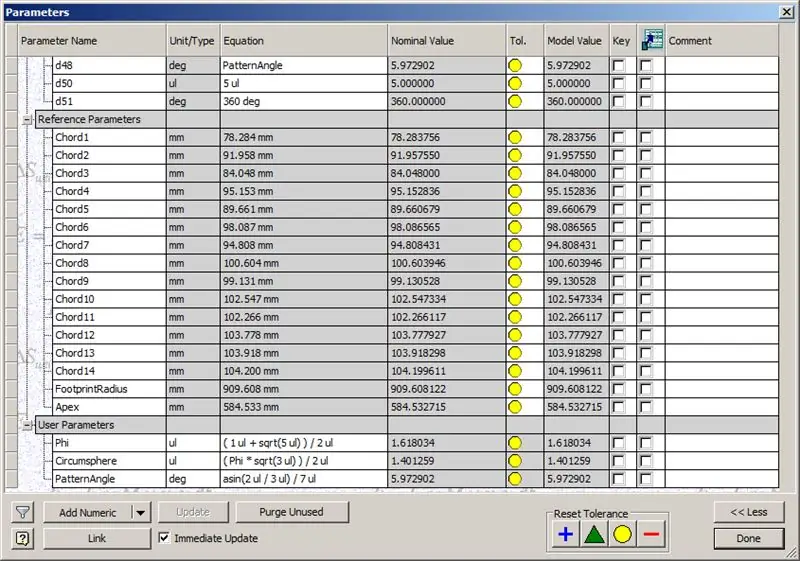
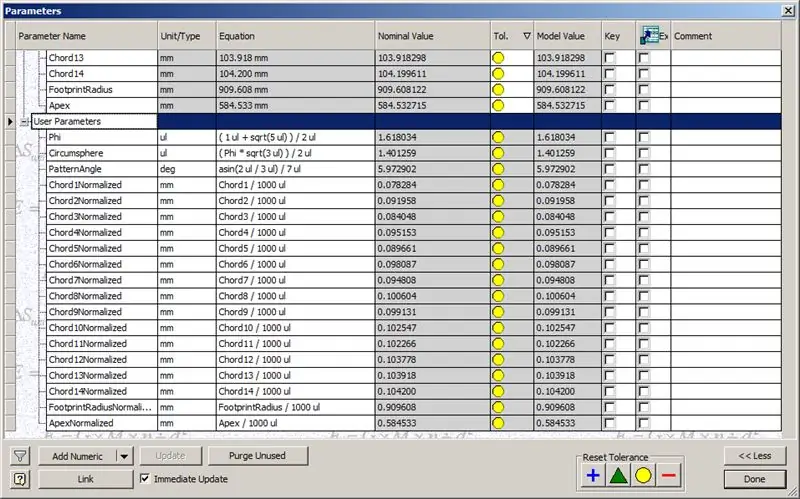
Quindi, la nostra cupola è finita, ma vediamo se i numeri corrispondono al modello di TaffGoch:

Seguendo i parametri di riferimento, sembra che siano una corrispondenza perfetta!

Dividendo le lunghezze delle corde per 1000, possiamo vedere chiaramente una corrispondenza perfetta con i fattori di corda del modello di TaffGoch, così come il raggio di impronta e i fattori di apice.