Osservare la prescrizione del bulbo oculare: un progetto BME60B: 9 passaggi

2024 Autore: John Day | [email protected]. Ultima modifica: 2024-01-30 10:00

Di: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

L'ingrandimento è una delle caratteristiche chiave presenti per gli occhiali da lettura, che sono classificati in base alla loro prescrizione di diottrie. Secondo la Michigan Technology University, una diottria è una lunghezza focale dell'obiettivo, solitamente misurata in mm, nell'unità di metri (Michigan Technology University). Poiché gli occhiali da lettura hanno lenti convesse, la lunghezza focale sarebbe positiva, facendo sì che anche le diottrie siano positive (HyperPhysics). La lunghezza focale aumenta man mano che la distanza tra l'oggetto si allontana dall'obiettivo vero e proprio, e questo porta le diottrie a diminuire poiché sono inversamente proporzionali. Pertanto, avere occhiali da lettura con diottrie aggiuntive aiuterebbe l'obiettivo a ingrandire la vista in modo che possa sembrare che la lunghezza focale sia inferiore aumentando il valore delle diottrie.

Il codice presentato sarà utilizzato per prevedere la diottria di una lente con prescrizione sconosciuta. Per calcolare la prescrizione vengono utilizzati due input: una fotografia dello sfondo controllato senza l'utilizzo di lenti e un'altra fotografia dello stesso sfondo ma attraverso l'obiettivo prescelto. Il programma misurerà la distorsione tra queste due fotografie. Da lì, saremo in grado di stimare le diottrie dell'obiettivo e produrre un risultato che l'utente potrà visualizzare.

Per questo Instructable, avrai bisogno di:

• Un motivo a scacchiera in bianco e nero stampato su un foglio di carta 11x8,5 pollici
• Una fotocamera con la capacità di bloccare la messa a fuoco
• Un treppiede o qualcosa di simile per fissare la fotocamera
• Varie prescrizioni di occhiali da lettura
• MATLAB

Passaggio 1: scatta foto

Per calcolare l'ingrandimento di un obiettivo, devi essere in grado di confrontarlo con le dimensioni effettive dell'oggetto. Per questo progetto, confronteremo un'immagine ingrandita con un'immagine di controllo.

Pertanto, il primo passo è scattare due foto della stessa immagine: la prima solo attraverso la fotocamera e la seconda attraverso l'obiettivo degli occhiali da lettura che si desidera testare.

Scatterai una foto di una scacchiera in bianco e nero di 8,5x11 pollici con una griglia di 1 pollice. Imposta la tua fotocamera a 11 pollici di distanza dalla scacchiera. Prima di scattare le foto, bloccare la messa a fuoco sulla scacchiera.

Scatta una foto della scacchiera senza gli occhiali da lettura. Quindi, senza muovere nulla, posiziona gli occhiali da lettura davanti alla fotocamera e scatta la seconda foto.

Assicurati che la posizione della fotocamera non si sposti tra uno scatto e l'altro. L'unica cosa che dovrebbe cambiare tra le due foto è la presenza della lente degli occhiali davanti alla fotocamera.

Quando hai finito con le foto, caricale sul tuo computer.

Passaggio 2: carica le immagini in MATLAB

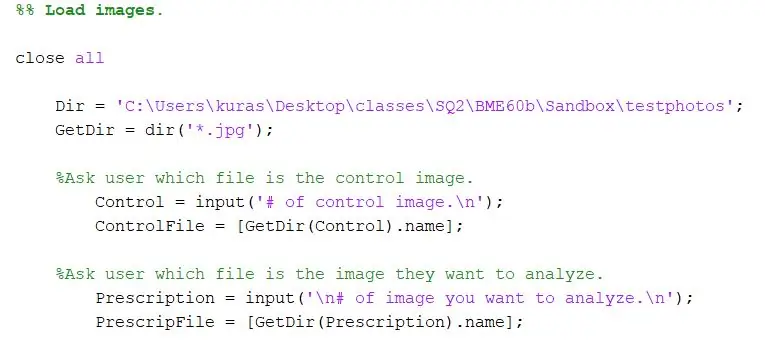
Apri un nuovo script.

Innanzitutto, specifica la directory in cui sono archiviate le foto. Quindi, usa la funzione dir per estrarre le immagini-j.webp

Dir = 'C:\Users\kuras\Desktop\classes\SQ2\BME60b\Sandbox\testphotos'; GetDir = dir('*.jpg');

Per il nostro progetto, volevamo chiedere all'utente del programma per quali file voleva confrontare. La prima sezione chiede all'utente di specificare l'immagine di controllo e la seconda chiede all'utente di specificare l'immagine di prova.

• %Chiedi all'utente quale file è l'immagine di controllo.
• Control = input('# di immagine di controllo.\n');
• ControlFile = [GetDir(Control).name]
• %Chiedi all'utente quale file è l'immagine che desidera analizzare.
• ChooseFile = input('\n# dell'immagine che vuoi analizzare.\n');
• PrescripFile = [GetDir(ScegliFile).name];

Passaggio 3: analisi dell'immagine

Un'immagine colorata in MATLAB è di dimensioni MxNx3, mentre un'immagine in scala di grigi è MxN. Ciò significa che è più veloce migliorare/modificare un'immagine in scala di grigi perché ci sono meno dati di cui tenere traccia. Usa rgb2gray per convertire l'immagine in scala di grigi. (La funzione imrotate è stata utilizzata perché le nostre foto sono arrivate in orizzontale - questa riga di codice potrebbe o non potrebbe essere necessaria nella tua versione.)

• %converti in scala di grigi e ruota
• I = imread(ControlFile);
• I = rgb2grigio(I);
• I = imrotate(I, 90);

Quindi, visualizza l'immagine. La funzione di sottotrama viene utilizzata in modo che l'immagine di prova possa essere accanto al controllo nei passaggi successivi.

• %Schermo
• Figura 1);
• sottotrama(1, 2, 1)
• imshow(I);
• titolo(ControlFile);

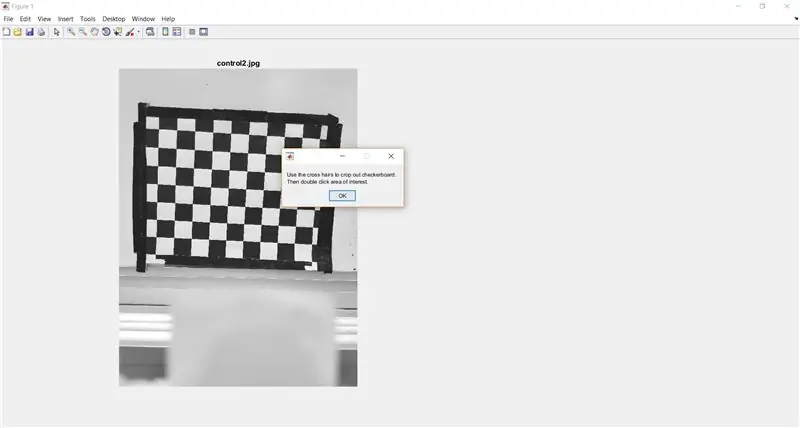
Usa imcrop per chiedere all'utente di ritagliare la scacchiera dall'immagine completa. Il codice seguente mostra anche una finestra di messaggio per fornire istruzioni all'utente.

• % ritaglia la scacchiera per l'analisi
• waitfor(msgbox({'Usa il mirino per ritagliare la scacchiera.', 'Quindi fai doppio clic sull'area di interesse.'}));
• I_crop = imcrop(I);

Usa imbinarize per binarizzare l'immagine.

I_binary = imbinarize(I_crop);

Passaggio 4: calcola la larghezza dei quadrati bianchi sulla scacchiera

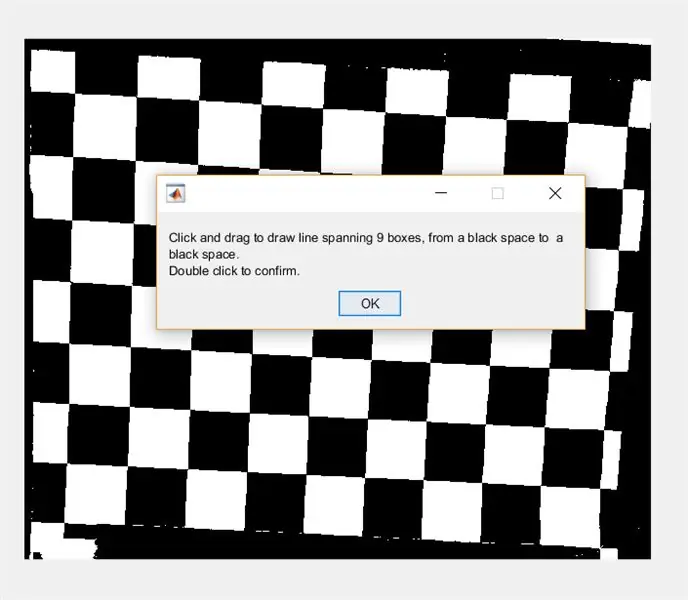
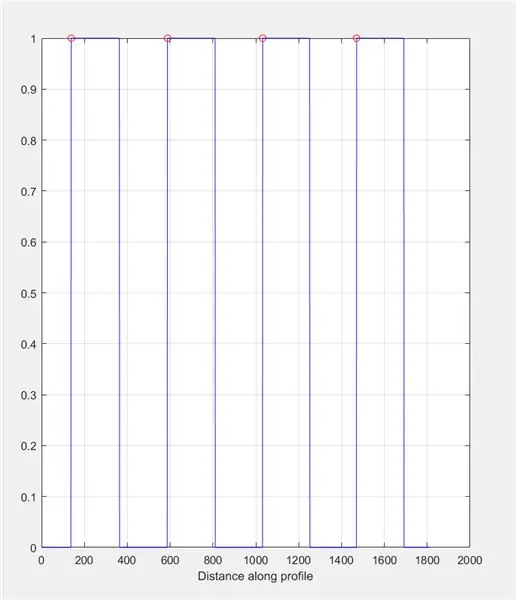
Quindi, chiedi all'utente di tracciare una linea attraverso l'immagine usando imline. Questa linea dovrebbe correre orizzontalmente attraverso la scacchiera. Dovrebbe iniziare e finire su un quadrato nero (non importa dove) - questo perché misureremo la larghezza dei quadrati bianchi, non di quelli neri.

• %disegnare la linea
• Figura 1)
• sottotrama(1, 2, 1)
• imshow(I_binario);
• waitfor(msgbox({'Fai clic e trascina per disegnare una linea che copre 9 caselle, da uno spazio nero a uno spazio nero.', 'Fai doppio clic per confermare.'}));
• linea = imline;
• posizione = attesa(linea);
• endpoints = line.getPosition;

Estrai le coordinate X e Y per i punti finali della linea disegnata.

• X = punti finali(:, 1)
• Y = estremi(:, 2);

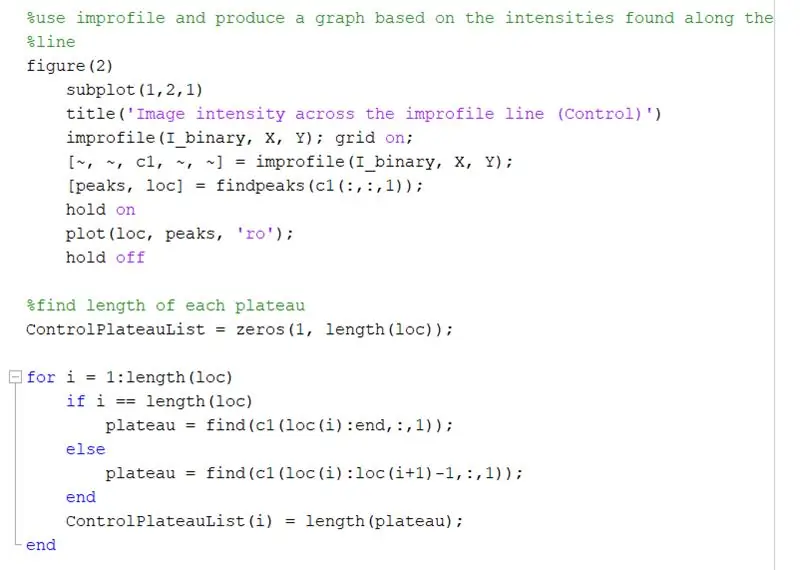
Usa improfile per produrre un grafico basato sulle intensità trovate lungo la linea disegnata. Dovrebbe assomigliare a un'onda quadra che va da 0 (nero) a 1 (bianco). Calcola anche i picchi e le loro posizioni.

• figura 2)
• sottotrama(1, 2, 1)
• title('Intensità dell'immagine attraverso la linea improfile (Control)')
• improfile(I_binario, X, Y); griglia attiva;
• [~, ~, c1, ~, ~] = improfile(I_binary, X, Y);
• [picchi, loc] = findpeaks(c1(:,:, 1));
• aspettare
• plot(loc, picchi, 'ro');
• tenere a bada

Trova la lunghezza di ogni plateau sul grafico improfile usando un ciclo for. Eseguire il ciclo for per la stessa quantità di picchi presenti nel grafico improfile. Per calcolare la lunghezza di ciascun plateau, utilizzare la funzione "trova" per trovare tutte le posizioni in cui è presente un valore di intensità "1" anziché "0". Quindi, calcola la lunghezza di quell'array per ottenere la lunghezza totale del plateau, che dovrebbe essere uguale alla larghezza di un quadrato bianco in pixel. ControlPlateauList = zeros(1, length(loc));

per i = 1:lunghezza(loc)

se io == lunghezza(loc)

plateau = find(c1(loc(i):end,:, 1));

altro

plateau = trova(c1(loc(i):loc(i+1)-1,:, 1));

fine

ControlPlateauList(i) = length(plateau);

fine

Passaggio 5: ripetere i passaggi 3 e 4 per l'immagine di prova

*Nota: quando si disegna la linea di profilo sull'immagine di prova, assicurarsi di disegnarla attraverso i quadrati che corrispondono alla linea disegnata sull'immagine di controllo.

Passaggio 6: calcolare l'ingrandimento dell'obiettivo

Le misurazioni ingrandite vengono calcolate dividendo la media della lunghezza del plateau, calcolata nel passaggio 5, per la media della lunghezza del plateau di controllo, calcolata nel passaggio 4. Questo valore è pari a 1,0884.

ingrandimento = mean(plateauList)/mean(ControlPlateauList);

Passaggio 7: trovare R-squared e la prescrizione dell'utente tramite interpolazione

Usando il codice:

• md1 = fitlm(GivenPrescription, MagArray);
• Rquadrato = md1. Rquadrato. Ordinario;

Possiamo trovare il valore R-quadrato del grafico GivenPresciption (valori dati dalle nostre lenti) rispetto a MagArray (una matrice dei rapporti di misurazione dell'ingrandimento che abbiamo calcolato in precedenza). Avendo un valore R-quadrato sufficientemente alto, si può dedurre che esiste una correlazione abbastanza forte da giustificare l'uso di questo metodo. Per questo caso particolare, il valore R-quadrato era 0,9912, il che suggerisce una forte correlazione e quindi è giustificato utilizzare questo metodo nell'analisi.

Utilizzando la funzione:

Prescrizione = interp1(MagArray, GivenPrescription, ingrandimento, 'lineare');

Possiamo interpolare il valore di prescrizione corrispondente (sull'asse x) del nostro rapporto di ingrandimento (un valore sull'asse y) e trovare qual è la prescrizione dell'utente.

L'interpolazione dei dati è importante affinché questo metodo funzioni in quanto ci consente di fare ipotesi su informazioni che non abbiamo, sulla base delle informazioni che abbiamo. Mentre una linea di migliore adattamento sarebbe tecnicamente un candidato più forte per questa ipotesi, la creazione di limiti per ridurre il numero di uscite ha lo stesso effetto degli occhiali da vista che hanno comunque valori uniformi incrementali. Questo è spiegato nei passaggi successivi.

Passaggio 8: mostrare la prescrizione dell'utente su un grafico

Utilizzando il seguente codice:

• figura;
• plot(GivenPrescription, MagArray, '-g')
• aspettare
• plot(Prescrizione, ingrandimento, 'bp')
• tenere a bada
• griglia
• legend('Dati', 'Punti interpolati', 'Località', 'NW')

Possiamo tracciare un grafico che mostra i rapporti di ingrandimento rispetto alla prescrizione data con una linea verde e i dati trovati del nostro ingrandimento calcolato rispetto alla nostra prescrizione interpolata con una stella blu. Quindi la legenda etichetta il titolo, l'asse x e l'asse y e posiziona la legenda nell'angolo in alto a sinistra.

Passaggio 9: restringere la prescrizione

Il codice seguente viene utilizzato per produrre l'arrotondamento per la prescrizione:

• se prescrizione <= 1.125

  CalculatedPrescription = '1.0';

• altrimenti se prescrizione <= 1.375

  Prescrizione calcolata = '1.25';

• elseif prescrizione <= 1.625

  CalculatedPrescription = '1.5';

• altrimenti se prescrizione <= 1.875

  CalculatedPrescription = '1.75';

• altrimenti se prescrizione <= 2.25

  CalculatedPrescription = '2.0';

• altrimenti se prescrizione <= 2.625

  CalculatedPrescription = '2.5';

• altrimenti se prescrizione <= 3

  Prescrizione calcolata = '2.75';

• altrimenti se prescrizione <= 3.375

  Prescrizione calcolata = '3.25';

• altro

  CalculatedPrescription = 'sconosciuto';

• fine

La prescrizione trovata attraverso l'interpolazione non riflette necessariamente la prescrizione effettiva - questo perché ci saranno sempre lievi variazioni nell'analisi della foto a causa di un errore umano. Pertanto, abbiamo bisogno di questo passaggio per classificare la prescrizione effettiva.

Le prescrizioni che vengono fornite di solito partono da 1,0 diottrie e aumentano di 0,25 nelle loro prescrizioni, quindi dopo aver calcolato la prescrizione vogliamo determinare la prescrizione più adatta a ciò di cui l'utente potrebbe aver bisogno. Dopo aver calcolato la prescrizione, eseguiamo le istruzioni If date per verificarne il valore e determinare quale prescrizione è necessaria. Qualsiasi cosa minore o uguale a 1,125, la prescrizione è 1,0. Qualsiasi cosa inferiore o uguale a 1,375, la prescrizione è 1,25. Qualsiasi cosa minore o uguale a 1,625, la prescrizione è 1,5. Qualsiasi cosa inferiore o uguale a 1,845, la prescrizione è 1,75. E così via.

Abbiamo i valori in aumento poiché stiamo controllando se i valori sono inferiori a. Se facessimo diminuire i valori, la prima istruzione if leggerebbe sempre la prima istruzione if. Se la prescrizione è la più piccola, vogliamo che la riconosca subito come la più piccola, ecco perché il valore più piccolo è quello con cui abbiamo iniziato. Qualsiasi valore superiore al valore più alto significa che la prescrizione non è nell'intervallo con i nostri dati, quindi darà la lettura della stringa "Sconosciuta".