
Sommario:
- Autore John Day day@howwhatproduce.com.
- Public 2024-01-30 10:06.
- Ultima modifica 2025-01-23 14:50.
introduzione
Questa guida è destinata a tutti coloro che sono interessati all'utilizzo di accelerometri e giroscopi, nonché di dispositivi IMU (Inertial Measurement Unit) combinati nei loro progetti di elettronica
Tratteremo:
- Cosa misura un accelerometro?
- Cosa misura un giroscopio (detto anche giroscopio)?
- Come convertire le letture da analogico a digitale (ADC) ottenute da questi sensori in unità fisiche (quelle sarebbero g per l'accelerometro, gradi/s per il giroscopio)
- Come combinare le letture dell'accelerometro e del giroscopio per ottenere informazioni accurate sull'inclinazione del dispositivo rispetto al piano terra
In tutto l'articolo cercherò di mantenere la matematica al minimo. Se sai cosa sono Seno/Coseno/Tangente, dovresti essere in grado di comprendere e utilizzare queste idee nel tuo progetto, indipendentemente dalla piattaforma che stai utilizzando: Arduino, Propeller, Basic Stamp, chip Atmel, Microchip PIC, ecc.
Ci sono persone là fuori che credono che sia necessaria una matematica complessa per utilizzare un'unità IMU (filtri FIR o IIR complessi come i filtri Kalman, i filtri Parks-McClellan, ecc.). Puoi ricercare tutti questi e ottenere risultati meravigliosi ma complessi. Il mio modo di spiegare le cose richiede solo matematica di base. Sono un grande sostenitore della semplicità. Penso che un sistema semplice sia più facile da controllare e monitorare, inoltre molti dispositivi embedded non hanno la potenza e le risorse per implementare algoritmi complessi che richiedono calcoli a matrice.
Userò come esempio una nuova unità IMU, l'Acc_Gyro Accelerometer + Gyro IMU. Useremo i parametri di questo dispositivo nei nostri esempi di seguito. Questa unità è un buon dispositivo con cui iniziare perché è composta da 2 dispositivi:
- LIS331AL (scheda tecnica) - un accelerometro triassiale 2G - LPR550AL (scheda tecnica) - un passo e rollio a due assi, giroscopio da 500 gradi/sec
Insieme rappresentano un'unità di misura inerziale a 5 gradi di libertà. Questo è un nome di fantasia! Tuttavia, dietro il nome di fantasia c'è un dispositivo combinato molto utile che tratteremo e spiegheremo in dettaglio in questa guida.
Passaggio 1: l'accelerometro
Per capire questa unità inizieremo con l'accelerometro. Quando si pensa agli accelerometri è spesso utile immaginare una scatola a forma di cubo con una palla al suo interno. Puoi immaginare qualcos'altro come un biscotto o una ciambella, ma immagino una palla:
Se prendiamo questa scatola in un luogo senza campi gravitazionali o comunque senza altri campi che potrebbero influenzare la posizione della palla, la palla galleggerà semplicemente nel mezzo della scatola. Puoi immaginare che la scatola sia nello spazio, molto molto lontano da qualsiasi corpo cosmico, o se un posto del genere è difficile da trovare, immagina almeno un'astronave in orbita attorno al pianeta dove tutto è in uno stato senza peso. Dall'immagine sopra puoi vedere che assegniamo ad ogni asse una coppia di muri (abbiamo rimosso il muro Y+ per poter guardare all'interno della scatola). Immagina che ogni parete sia sensibile alla pressione. Se spostiamo improvvisamente la scatola a sinistra (la acceleriamo con accelerazione 1g = 9,8m/s^2), la palla colpirà il muro X-. Quindi misuriamo la forza di pressione che la palla applica alla parete e emettiamo un valore di -1 g sull'asse X.
Si noti che l'accelerometro rileverà effettivamente una forza diretta nella direzione opposta al vettore di accelerazione. Questa forza è spesso chiamata forza inerziale o forza fittizia. Una cosa che dovresti imparare da questo è che un accelerometro misura l'accelerazione indirettamente attraverso una forza applicata a una delle sue pareti (secondo il nostro modello, potrebbe essere una molla o qualcos'altro negli accelerometri della vita reale). Questa forza può essere causata dall'accelerazione, ma come vedremo nel prossimo esempio non è sempre causata dall'accelerazione.
Se prendiamo il nostro modello e lo mettiamo sulla Terra, la pallina cadrà sulla parete Z e applicherà una forza di 1 g sulla parete inferiore, come mostrato nell'immagine qui sotto:
In questo caso la scatola non si muove ma otteniamo comunque una lettura di -1g sull'asse Z. La pressione che la palla ha applicato sul muro è stata causata da una forza gravitazionale. In teoria potrebbe essere un diverso tipo di forza: ad esempio, se immagini che la nostra palla sia metallica, posizionare un magnete accanto alla scatola potrebbe spostare la palla in modo che colpisca un altro muro. Questo è stato detto solo per dimostrare che in sostanza l'accelerometro misura la forza non l'accelerazione. Succede semplicemente che l'accelerazione provochi una forza inerziale che viene catturata dal meccanismo di rilevamento della forza dell'accelerometro.
Sebbene questo modello non sia esattamente il modo in cui è costruito un sensore MEMS, è spesso utile per risolvere i problemi relativi all'accelerometro. Esistono in realtà sensori simili che hanno sfere metalliche all'interno, sono chiamati interruttori di inclinazione, tuttavia sono più primitivi e di solito possono solo dire se il dispositivo è inclinato entro un certo raggio o meno, non l'entità dell'inclinazione.
Finora abbiamo analizzato l'uscita dell'accelerometro su un singolo asse e questo è tutto ciò che otterrai con gli accelerometri a singolo asse. Il vero valore degli accelerometri triassiali deriva dal fatto che possono rilevare le forze d'inerzia su tutti e tre gli assi. Torniamo al nostro modello di scatola e ruotiamo la scatola di 45 gradi a destra. La palla toccherà ora 2 muri: Z- e X- come mostrato nell'immagine qui sotto:
I valori di 0,71 non sono arbitrari, sono in realtà un'approssimazione per SQRT(1/2). Questo diventerà più chiaro quando introdurremo il nostro prossimo modello per l'accelerometro.
Nel modello precedente abbiamo fissato la forza gravitazionale e ruotato la nostra scatola immaginaria. Negli ultimi 2 esempi abbiamo analizzato l'output in 2 diverse posizioni del riquadro, mentre il vettore di forza è rimasto costante. Anche se questo è stato utile per capire come l'accelerometro interagisce con le forze esterne, è più pratico eseguire calcoli se fissiamo il sistema di coordinate agli assi dell'accelerometro e immaginiamo che il vettore di forza ruoti intorno a noi.
Si prega di dare un'occhiata al modello sopra, ho conservato i colori degli assi in modo da poter effettuare un passaggio mentale dal modello precedente a quello nuovo. Immagina solo che ogni asse nel nuovo modello sia perpendicolare alle rispettive facce della scatola nel modello precedente. Il vettore R è il vettore di forza che l'accelerometro sta misurando (potrebbe essere la forza gravitazionale o la forza d'inerzia degli esempi sopra o una combinazione di entrambe). Rx, Ry, Rz sono proiezioni del vettore R sugli assi X, Y, Z. Si prega di notare la seguente relazione:
R^2 = Rx^2 + Ry^2 + Rz^2 (Eq. 1)
che è fondamentalmente l'equivalente del teorema di Pitagora in 3D.
Ricorda che poco prima ti ho detto che i valori di SQRT(1/2) ~ 0,71 non sono casuali. Se li inseriamo nella formula sopra, dopo aver ricordato che la nostra forza gravitazionale era di 1 g possiamo verificare che:
1^2 = (-QUADRATO(1/2))^2 + 0 ^2 + (-QUADRATO(1/2))^2
semplicemente sostituendo R=1, Rx = -SQRT(1/2), Ry = 0, Rz = -SQRT(1/2) nell'Eq.1
Dopo un lungo preambolo di teoria ci stiamo avvicinando agli accelerometri della vita reale. I valori Rx, Ry, Rz sono in realtà correlati linearmente ai valori emessi dal tuo accelerometro reale e che puoi utilizzare per eseguire vari calcoli.
Prima di arrivarci, parliamo un po' del modo in cui gli accelerometri ci forniranno queste informazioni. La maggior parte degli accelerometri rientra in due categorie: digitali e analogici. Gli accelerometri digitali ti forniranno informazioni utilizzando un protocollo seriale come I2C, SPI o USART, mentre gli accelerometri analogici emetteranno un livello di tensione all'interno di un intervallo predefinito che devi convertire in un valore digitale utilizzando un modulo ADC (convertitore da analogico a digitale). Non entrerò nei dettagli su come funziona l'ADC, in parte perché è un argomento così vasto e in parte perché è diverso da una piattaforma all'altra. Alcuni microcontrollori avranno moduli ADC incorporati, alcuni di essi avranno bisogno di componenti esterni per eseguire le conversioni ADC. Indipendentemente dal tipo di modulo ADC che utilizzi, ti ritroverai con un valore in un determinato intervallo. Ad esempio, un modulo ADC a 10 bit emetterà un valore nell'intervallo 0..1023, notare che 1023 = 2^10 -1. Un modulo ADC a 12 bit emetterà un valore nell'intervallo 0..4095, si noti che 4095 = 2^12-1.
Andiamo avanti considerando un semplice esempio, supponiamo che il nostro modulo ADC a 10 bit ci abbia fornito i seguenti valori per i tre canali dell'accelerometro (assi):
AdcRx = 586 AdcRy = 630 AdcRz = 561
Ogni modulo ADC avrà una tensione di riferimento, supponiamo nel nostro esempio che sia 3,3V. Per convertire un valore adc a 10 bit in tensione utilizziamo la seguente formula:
VoltRx = AdcRx * Vref / 1023
Una breve nota qui: che per l'ADC a 8 bit l'ultimo divisore sarebbe 255 = 2 ^ 8 -1 e per l'ADC a 12 bit l'ultimo divisore sarebbe 4095 = 2^12 -1.
Applicando questa formula a tutti e 3 i canali otteniamo:
VoltsRx = 586 * 3.3V / 1023 =~ 1.89V (arrotondamo tutti i risultati a 2 punti decimali) VoltsRy = 630 * 3.3V / 1023 =~ 2.03V VoltsRz = 561 * 3.3V / 1023 =~ 1.81V
Ogni accelerometro ha un livello di tensione zero g, lo trovi nelle specifiche, questa è la tensione che corrisponde a 0 g. Per ottenere un valore di tensione con segno dobbiamo calcolare lo spostamento da questo livello. Diciamo che il nostro livello di tensione 0g è VzeroG = 1,65V. Calcoliamo gli spostamenti di tensione dalla tensione zero-g come segue:
DeltaVoltsRx = 1,89V - 1,65V = 0,24V DeltaVoltsRy = 2,03V - 1,65V = 0,38V DeltaVoltsRz = 1,81V - 1,65V = 0,16V
Ora abbiamo le letture dell'accelerometro in Volt, non è ancora in g (9,8 m/s^2), per fare la conversione finale applichiamo la sensibilità dell'accelerometro, solitamente espressa in mV/g. Diciamo che la nostra sensibilità = 478,5 mV/g = 0,4785 V/g. I valori di sensibilità possono essere trovati nelle specifiche dell'accelerometro. Per ottenere i valori di forza finali espressi in g utilizziamo la seguente formula:
Rx = DeltaVoltsRx / Sensibilità
Rx = 0,24 V / 0,4785 V/g =~ 0,5 g Ry = 0,38 V / 0,4785 V/g = ~ 0,79 g Rz = 0,16 V / 0,4785 V/g =~ 0,33 g
Potremmo ovviamente combinare tutti i passaggi in un'unica formula, ma ho seguito tutti i passaggi per chiarire come si passa dalle letture ADC a un componente del vettore di forza espresso in g.
Rx = (AdcRx * Vref / 1023 - VzeroG) / Sensibilità (Eq.2) Ry = (AdcRy * Vref / 1023 - VzeroG) / Sensibilità Rz = (AdcRz * Vref / 1023 - VzeroG) / Sensibilità
Ora abbiamo tutte e 3 le componenti che definiscono il nostro vettore di forza d'inerzia, se il dispositivo non è soggetto ad altre forze diverse dalla gravitazione, possiamo assumere che questa sia la direzione del nostro vettore di forza di gravità. Se vuoi calcolare l'inclinazione del dispositivo rispetto al suolo puoi calcolare l'angolo tra questo vettore e l'asse Z. Se sei interessato anche alla direzione di inclinazione per asse puoi dividere questo risultato in 2 componenti: inclinazione sull'asse X e Y che può essere calcolata come l'angolo tra il vettore di gravitazione e gli assi X/Y. Calcolare questi angoli è più semplice di quanto si possa pensare, ora che abbiamo calcolato i valori per Rx, Ry e Rz. Torniamo al nostro ultimo modello di accelerometro e facciamo alcune notazioni aggiuntive:
Gli angoli che ci interessano sono gli angoli tra gli assi X, Y, Z e il vettore di forza R. Definiremo questi angoli come Axr, Ayr, Azr. Puoi notare dal triangolo rettangolo formato da R e Rx che:
cos(Axr) = Rx / R, e similmente: cos(Ayr) = Ry / R cos(Azr) = Rz / R
Possiamo dedurre dall'Eq.1 che R = SQRT(Rx^2 + Ry^2 + Rz^2).
Ora possiamo trovare i nostri angoli usando la funzione arccos() (la funzione inversa cos()):
Axr = arccos(Rx/R) Ayr = arccos(Ry/R) Azr = arccos(Rz/R)
Abbiamo fatto molta strada per spiegare il modello dell'accelerometro, solo per arrivare a queste formule. A seconda delle applicazioni, potresti voler utilizzare le formule intermedie che abbiamo derivato. Presto introdurremo anche il modello del giroscopio e vedremo come i dati dell'accelerometro e del giroscopio possono essere combinati per fornire stime dell'inclinazione ancora più accurate.
Ma prima di farlo, facciamo alcune notazioni più utili:
cosX = cos(Axr) = Rx / R cosy = cos(Ayr) = Ry / R cosZ = cos(Azr) = Rz / R
Questa tripletta è spesso chiamata direzione coseno e rappresenta fondamentalmente il vettore unitario (vettore con lunghezza 1) che ha la stessa direzione del nostro vettore R. Puoi facilmente verificare che:
SQRT(cosX^2 + cosY^2 + cosZ^2) = 1
Questa è una bella proprietà poiché ci assolve dal monitoraggio del modulo (lunghezza) del vettore R. Spesso, se siamo interessati solo alla direzione del nostro vettore inerziale, ha senso normalizzarne il modulo per semplificare altri calcoli.
Passaggio 2: giroscopio
Non introdurremo alcun modello di scatola equivalente per il giroscopio come abbiamo fatto per l'accelerometro, ma passeremo direttamente al secondo modello di accelerometro e mostreremo cosa misura il giroscopio secondo questo modello.
Ciascun canale del giroscopio misura la rotazione attorno a uno degli assi. Ad esempio un giroscopio a 2 assi misurerà la rotazione attorno (o qualcuno potrebbe dire "circa") gli assi X e Y. Per esprimere questa rotazione in numeri facciamo alcune notazioni. Per prima cosa definiamo:
Rxz - è la proiezione del vettore di forza d'inerzia R sul piano XZ Ryz - è la proiezione del vettore di forza d'inerzia R sul piano YZ
Dal triangolo rettangolo formato da Rxz e Rz, utilizzando il teorema di Pitagora si ottiene:
Rxz^2 = Rx^2 + Rz^2 e allo stesso modo: Ryz^2 = Ry^2 + Rz^2
si noti inoltre che:
R^2 = Rxz^2 + Ry^2, questo può essere derivato dall'Eq.1 e dalle equazioni precedenti, oppure può essere derivato dal triangolo rettangolo formato da R e Ryz R^2 = Ryz^2 + Rx^2
Non useremo queste formule in questo articolo, ma è utile notare la relazione tra tutti i valori nel nostro modello.
Invece andremo a definire l'angolo tra l'asse Z e i vettori Rxz, Ryz come segue:
Axz - è l'angolo tra Rxz (proiezione di R sul piano XZ) e l'asse Z Ayz - è l'angolo tra Ryz (proiezione di R sul piano YZ) e l'asse Z
Ora ci stiamo avvicinando a ciò che misura il giroscopio. Il giroscopio misura la velocità di variazione degli angoli definiti sopra. In altre parole produrrà un valore che è correlato linearmente alla velocità di variazione di questi angoli. Per spiegarlo, supponiamo di aver misurato l'angolo di rotazione attorno all'asse Y (che sarebbe l'angolo Axz) al tempo t0, e lo definiamo come Axz0, quindi abbiamo misurato questo angolo in un secondo momento t1 ed era Axz1. Il tasso di cambio sarà calcolato come segue:
RateAxz = (Axz1 - Axz0) / (t1 - t0).
Se esprimiamo Axz in gradi e tempo in secondi, allora questo valore sarà espresso in gradi/s. Questo è ciò che misura un giroscopio.
In pratica un giroscopio (a meno che non sia un giroscopio digitale speciale) raramente ti darà un valore espresso in gradi/s. Come per l'accelerometro, otterrai un valore ADC che dovrai convertire in gradi/s usando una formula simile all'Eq. 2 che abbiamo definito per l'accelerometro. Introduciamo la formula di conversione da ADC a gradi/s per il giroscopio (supponiamo di utilizzare un modulo ADC a 10 bit, per ADC a 8 bit sostituire 1023 con 255, per ADC a 12 bit sostituire 1023 con 4095).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensibilità Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Sensibilità
AdcGyroXZ, AdcGyroYZ - sono ottenuti dal nostro modulo adc e rappresentano i canali che misurano la rotazione della proiezione del vettore R in XZ rispettivamente nei piani YZ, che equivale a dire che la rotazione è stata eseguita rispettivamente attorno agli assi Y e X.
Vref - è la tensione di riferimento dell'ADC che useremo 3.3V nell'esempio sotto VzeroRate - è la tensione a tasso zero, ovvero la tensione che emette il giroscopio quando non è soggetto ad alcuna rotazione, per la scheda Acc_Gyro è ad esempio 1.23V (puoi trovare questo valore nelle specifiche) Sensibilità - è la sensibilità del tuo giroscopio è espressa in mV / (gradi / s) spesso scritto come mV/gradi/s, sostanzialmente ti dice quanti mV l'uscita del giroscopio aumenta se si aumenta la velocità di rotazione di un grado/s. La sensibilità della scheda Acc_Gyro è ad esempio 2mV/deg/s o 0.002V/deg/s
Facciamo un esempio, supponiamo che il nostro modulo ADC abbia restituito i seguenti valori:
AdcGyroXZ = 571 AdcGyroXZ = 323
Usando la formula sopra e usando i parametri delle specifiche della scheda Acc_Gyro otterremo:
RateAxz = (571 * 3,3 V / 1023 - 1,23 V) / (0,002 V/deg/s) =~ 306 gradi/s RateAyz = (323 * 3,3 V / 1023 - 1,23 V) / (0,002 V/deg/s) =~ -94 gradi/s
In altre parole il dispositivo ruota attorno all'asse Y (o possiamo dire che ruota nel piano XZ) con una velocità di 306 gradi/se attorno all'asse X (o possiamo dire che ruota nel piano YZ) con una velocità di - 94 gradi/s. Si prega di notare che il segno negativo significa che il dispositivo ruota nella direzione opposta rispetto alla direzione positiva convenzionale. Per convenzione un senso di rotazione è positivo. Un buon foglio delle specifiche del giroscopio ti mostrerà quale direzione è positiva, altrimenti dovrai trovarla sperimentando con il dispositivo e notando quale direzione di rotazione provoca un aumento della tensione sul pin di uscita. È meglio farlo utilizzando un oscilloscopio poiché non appena si interrompe la rotazione, la tensione tornerà al livello di velocità zero. Se stai usando un multimetro dovresti mantenere una velocità di rotazione costante per almeno alcuni secondi e annotare la tensione durante questa rotazione, quindi confrontarla con la tensione a velocità zero. Se è maggiore della tensione a tasso zero significa che il senso di rotazione è positivo.
Passaggio 3: combinazione dell'accelerometro e del giroscopio
Mettere tutto insieme - Combinare i dati dell'accelerometro e del giroscopio
Se stai leggendo questo articolo, probabilmente hai acquistato o stai pianificando di acquisire un dispositivo IMU, o probabilmente stai pianificando di costruirne uno da dispositivi accelerometro e giroscopio separati.
Il primo passo nell'utilizzo di un dispositivo IMU combinato che combina un accelerometro e un giroscopio è allineare i loro sistemi di coordinate. Il modo più semplice per farlo è scegliere il sistema di coordinate dell'accelerometro come sistema di coordinate di riferimento. La maggior parte dei fogli dati dell'accelerometro mostrerà la direzione degli assi X, Y, Z rispetto all'immagine del chip o dispositivo fisico. Ad esempio, ecco le direzioni degli assi X, Y, Z come mostrato nelle specifiche per la scheda Acc_Gyro:
I prossimi passi sono:
Identificare le uscite del giroscopio che corrispondono ai valori RateAxz, RateAyz discussi sopra. Determinare se queste uscite devono essere invertite a causa della posizione fisica del giroscopio rispetto all'accelerometro
Non dare per scontato che se un giroscopio ha un'uscita contrassegnata con X o Y, corrisponderà a qualsiasi asse nel sistema di coordinate dell'accelerometro, anche se questa uscita fa parte di un'unità IMU. Il modo migliore è testarlo. Supponendo che tu abbia fissato la posizione del giroscopio rispetto all'accelerometro. Si presume che i bordi del giroscopio e dell'accelerometro siano paralleli tra loro, ovvero si posiziona il giroscopio a un angolo multiplo di 90 gradi rispetto al chip dell'accelerometro. Se hai acquisito una scheda IMU, è probabile che siano già allineati in questo modo. Non discuteremo in questo articolo i modelli in cui il giroscopio è posizionato con un angolo irregolare rispetto all'accelerometro (diciamo 45 o 30 gradi), anche se questo potrebbe essere utile in alcune applicazioni.
Ecco una sequenza di esempio per determinare quale uscita del giroscopio corrisponde al valore RateAxz discusso sopra.
- iniziare dal posizionare il dispositivo in posizione orizzontale. Entrambe le uscite X e Y dell'accelerometro emetterebbero la tensione zero-g (ad esempio per la scheda Acc_Gyro questo è 1,65 V)
- poi inizia a ruotare il dispositivo attorno all'asse Y, un altro modo per dirlo è che ruoti il dispositivo sul piano XZ, in modo che le uscite dell'accelerometro X e Z cambino e l'uscita Y rimanga costante. - durante la rotazione del dispositivo a velocità costante notare quale uscita del giroscopio cambia, le altre uscite del giroscopio dovrebbero rimanere costanti - l'uscita del giroscopio che è cambiata durante la rotazione attorno all'asse Y (rotazione nel piano XZ) fornirà il valore di ingresso per AdcGyroXZ, da cui calcoliamo RateAxz - il passo finale è assicurarsi che il senso di rotazione corrisponda al nostro modello, in alcuni casi potrebbe essere necessario invertire il valore RateAxz a causa della posizione fisica del giroscopio rispetto all'accelerometro - eseguire nuovamente il test sopra, ruotando il dispositivo intorno l'asse Y, questa volta monitora l'uscita X dell'accelerometro (AdcRx nel nostro modello). Se AdcRx cresce (i primi 90 gradi di rotazione dalla posizione orizzontale), anche AdcGyroXZ dovrebbe crescere. Altrimenti devi invertire RateAxz, puoi farlo introducendo un fattore di segno nell'Eq.3, come segue:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivity, dove InvertAxz è 1 o -1
stesso test può essere fatto per RateAyz, ruotando il dispositivo attorno all'asse X, e puoi identificare quale uscita del giroscopio corrisponde a RateAyz e se deve essere invertita. Una volta ottenuto il valore di InvertAyz, dovresti utilizzare la seguente formula per calcolare RateAyz:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / Sensibilità
Se eseguissi questi test sulla scheda Acc_Gyro otterresti i seguenti risultati:
- il pin di uscita per RateAxz è GX4 e InvertAxz = -1. - il pin di uscita per RateAyz è GY4 e InvertAyz = -1
Da questo punto in poi considereremo che hai impostato la tua IMU in modo tale da poter calcolare i valori corretti per Axr, Ayr, Azr (come definito nella Parte 1. Accelerometro) e RateAxz, RateAyz (come definito nella Parte 2. Giroscopio). Successivamente analizzeremo le relazioni tra questi valori che risultano utili per ottenere una stima più accurata dell'inclinazione del dispositivo rispetto al piano terra.
Potresti chiederti a questo punto, se il modello dell'accelerometro ci ha già fornito angoli di inclinazione di Axr, Ayr, Azr, perché dovremmo preoccuparci dei dati del giroscopio? La risposta è semplice: i dati dell'accelerometro non possono essere sempre attendibili al 100%. Ci sono diverse ragioni, ricorda che l'accelerometro misura la forza d'inerzia, tale forza può essere causata dalla gravitazione (e idealmente solo dalla gravitazione), ma potrebbe anche essere causata dall'accelerazione (movimento) del dispositivo. Di conseguenza, anche se l'accelerometro è in uno stato relativamente stabile, è ancora molto sensibile alle vibrazioni e al rumore meccanico in generale. Questo è il motivo principale per cui la maggior parte dei sistemi IMU utilizza un giroscopio per appianare eventuali errori dell'accelerometro. Ma come si fa? E il giroscopio è esente da rumore?
Il giroscopio non è esente da rumore tuttavia poiché misura la rotazione è meno sensibile ai movimenti meccanici lineari, il tipo di rumore che soffre l'accelerometro, tuttavia i giroscopi hanno altri tipi di problemi come ad esempio la deriva (non ritorno al valore di zero rate quando la rotazione si ferma). Tuttavia, calcolando la media dei dati provenienti dall'accelerometro e dal giroscopio, possiamo ottenere una stima relativamente migliore dell'inclinazione attuale del dispositivo rispetto a quella che otterremmo utilizzando i soli dati dell'accelerometro.
Nei prossimi passaggi introdurrò un algoritmo che è stato ispirato da alcune idee utilizzate nel filtro di Kalman, tuttavia è di gran lunga più semplice e facile da implementare su dispositivi embedded. Prima di ciò vediamo prima cosa vogliamo che il nostro algoritmo calcoli. Ebbene, è la direzione del vettore della forza gravitazionale R = [Rx, Ry, Rz] da cui possiamo derivare altri valori come Axr, Ayr, Azr o cosX, cosY, cosZ che ci daranno un'idea dell'inclinazione del nostro dispositivo rispetto al piano terra, discutiamo la relazione tra questi valori nella Parte 1. Si potrebbe dire: non abbiamo già questi valori Rx, Ry, Rz dall'Eq.2 nella Parte 1 ? Ebbene sì, ma ricorda che questi valori sono derivati solo dai dati dell'accelerometro, quindi se volessi usarli direttamente nella tua applicazione potresti ottenere più rumore di quanto la tua applicazione possa tollerare. Per evitare ulteriore confusione, ridefiniamo le misurazioni dell'accelerometro come segue:
Racc - è il vettore di forza inerziale misurato dall'accelerometro, che consiste delle seguenti componenti (proiezioni sugli assi X, Y, Z):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Sensibilità RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Sensibilità RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Sensibilità
Finora abbiamo una serie di valori misurati che possiamo ottenere esclusivamente dai valori ADC dell'accelerometro. Chiameremo questo insieme di dati un "vettore" e useremo la seguente notazione.
Racc = [RxAcc, RyAcc, RzAcc]
Poiché questi componenti di Racc possono essere ottenuti dai dati dell'accelerometro, possiamo considerarli un input per il nostro algoritmo.
Nota che poiché Racc misura la forza gravitazionale, avrai ragione se assumi che la lunghezza di questo vettore definito come segue sia uguale o vicina a 1 g.
|Racc| = SQRT(RxAcc^2 +RyAcc^2 + RzAcc^2), Tuttavia, per essere sicuri, ha senso aggiornare questo vettore come segue:
Racc(normalizzato) = [RxAcc/|Racc|, RyAcc/|Racc|, RzAcc/|Racc|].
Ciò garantirà che la lunghezza del vettore Racc normalizzato sia sempre 1.
Successivamente introdurremo un nuovo vettore e lo chiameremo
Riposo = [RxEst, RyEst, RzEst]
Questo sarà l'output del nostro algoritmo, questi sono valori corretti basati sui dati del giroscopio e basati su dati stimati passati.
Ecco cosa farà il nostro algoritmo: - l'accelerometro ci dice: "Sei in posizione Racc" - diciamo "Grazie, ma fammi controllare", - quindi correggi queste informazioni con i dati del giroscopio e con i dati di riposo passati e emettiamo un nuovo vettore stimato Rest. - consideriamo Rest la nostra "scommessa migliore" per quanto riguarda la posizione attuale del dispositivo.
Vediamo come possiamo farlo funzionare.
Inizieremo la nostra sequenza fidandoci del nostro accelerometro e assegnando:
Resto(0) = Racc(0)
A proposito, ricorda che Rest e Racc sono vettori, quindi l'equazione sopra è solo un modo semplice per scrivere 3 serie di equazioni ed evitare la ripetizione:
RxEst(0) = RxAcc(0) RyEst(0) = RyAcc(0) RzEst(0) = RzAcc(0)
Quindi faremo misurazioni regolari a intervalli di tempo uguali di T secondi e otterremo nuove misurazioni che definiremo come Racc(1), Racc(2), Racc(3) e così via. Emetteremo anche nuove stime ad ogni intervallo di tempo Rest(1), Rest(2), Rest(3) e così via.
Supponiamo di essere al passo n. Abbiamo due insiemi noti di valori che vorremmo usare:
Rest(n-1) - la nostra stima precedente, con Rest(0) = Racc(0) Racc(n) - la nostra attuale misurazione dell'accelerometro
Prima di poter calcolare Rest(n), introduciamo un nuovo valore misurato, che possiamo ricavare dal nostro giroscopio e da una stima precedente.
Lo chiameremo Rgyro, ed è anche un vettore composto da 3 componenti:
Rgyro = [RxGyro, RyGyro, RzGyro]
Calcoleremo questo vettore un componente alla volta. Inizieremo con RxGyro.
Iniziamo osservando la seguente relazione nel nostro modello di giroscopio, dal triangolo rettangolo formato da Rz e Rxz possiamo ricavare che:
tan(Axz) = Rx/Rz => Axz = atan2(Rx, Rz)
Atan2 potrebbe essere una funzione che non hai mai usato prima, è simile ad atan, tranne che restituisce valori nell'intervallo di (-PI, PI) anziché (-PI/2, PI/2) come restituito da atan, e richiede 2 argomenti invece di uno. Ci consente di convertire i due valori di Rx, Rz in angoli nell'intero intervallo di 360 gradi (da -PI a PI). Puoi leggere di più su atan2 qui.
Quindi conoscendo RxEst(n-1) e RzEst(n-1) possiamo trovare:
Axz(n-1) = atan2(RxEst(n-1), RzEst(n-1)).
Ricorda che il giroscopio misura la velocità di variazione dell'angolo Axz. Quindi possiamo stimare il nuovo angolo Axz(n) come segue:
Axz(n) = Axz(n-1) + RateAxz(n) * T
Ricorda che RateAxz può essere ottenuto dalle letture ADC del nostro giroscopio. Una formula più precisa può utilizzare una velocità di rotazione media calcolata come segue:
RateAxzAvg = (RateAxz(n) + RateAxz(n-1)) / 2 Axz(n) = Axz(n-1) + RateAxzAvg * T
Allo stesso modo possiamo trovare:
Ayz(n) = Ayz(n-1) + RateAyz(n) * T
Ok, ora abbiamo Axz(n) e Ayz(n). Dove andiamo da qui per detrarre RxGyro/RyGyro? Dall'eq. 1 possiamo scrivere la lunghezza del vettore Rgyro come segue:
|Rgyro| = SQRT(RxGyro^2 + RyGyro^2 + RzGyro^2)
Anche perché abbiamo normalizzato il nostro vettore Racc, possiamo supporre che la sua lunghezza sia 1 e non sia cambiata dopo la rotazione, quindi è relativamente sicuro scrivere:
|Rgyro| = 1
Adottiamo una notazione temporanea più breve per i calcoli seguenti:
x =RxGyro, y=RyGyro, z=RzGyro
Usando le relazioni precedenti possiamo scrivere:
x = x / 1 = x / RADQ(x^2+y^2+z^2)
Dividiamo numeratore e denominatore della frazione per SQRT(x^2 + z^2)
x = (x / SQRT(x^2 + z^2)) / SQRT((x^2 + y^2 + z^2) / (x^2 + z^2))
Nota che x / SQRT(x^2 + z^2) = sin(Axz), quindi:
x = sin(Axz) / SQRT (1 + y^2 / (x^2 + z^2))
Ora moltiplica numeratore e denominatore della frazione all'interno di SQRT per z^2
x = sin(Axz) / SQRT (1 + y^2 * z ^2 / (z^2 * (x^2 + z^2)))
Nota che z / SQRT(x^2 + z^2) = cos(Axz) e y / z = tan(Ayz), quindi infine:
x = sin(Axz) / SQRT (1 + cos(Axz)^2 * tan(Ayz)^2)
Tornando alla nostra notazione otteniamo:
RxGyro = sin(Axz(n)) / SQRT (1 + cos(Axz(n))^2 * tan(Ayz(n))^2)
allo stesso modo troviamo che
RyGyro = sin(Ayz(n)) / SQRT (1 + cos(Ayz(n))^2 * tan(Axz(n))^2)
Ora finalmente possiamo trovare:
RzGyro = Sign(RzGyro)*SQRT(1 - RxGyro^2 - RyGyro^2).
Dove Sign(RzGyro) = 1 quando RzGyro>=0 e Sign(RzGyro) = -1 quando RzGyro<0.
Un modo semplice per stimare questo è prendere:
Sign(RzGyro) = Sign(RzEst(n-1))
In pratica, fai attenzione quando RzEst(n-1) è vicino a 0. In questo caso puoi saltare del tutto la fase del giroscopio e assegnare: RzEst(n-1). Rz viene utilizzato come riferimento per il calcolo degli angoli Axz e Ayz e quando è vicino a 0, i valori possono traboccare e generare risultati errati. Sarai nel dominio di grandi numeri in virgola mobile in cui le implementazioni della funzione tan() / atan() potrebbero mancare di precisione.
Quindi ricapitoliamo quello che abbiamo finora, siamo al passaggio n del nostro algoritmo e abbiamo calcolato i seguenti valori:
Racc - letture correnti dal nostro accelerometro Rgyro - ottenute da Rest(n-1) e letture correnti del giroscopio
Quali valori utilizziamo per calcolare la stima aggiornata Rest(n) ? Probabilmente hai indovinato che useremo entrambi. Useremo una media ponderata, in modo che:
Riposo(n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
Possiamo semplificare questa formula dividendo sia il numeratore che il denominatore della frazione per w1.
Riposo(n) = (Racc * w1/w1 + Rgyro * w2/w1) / (w1/w1 + w2/w1)
e dopo aver sostituito w2/w1 = wGyro otteniamo:
Rest(n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
Nella precedente forumula wGyro ci dice quanto ci fidiamo del nostro giroscopio rispetto al nostro accelerometro. Questo valore può essere scelto sperimentalmente di solito valori compresi tra 5..20 innescheranno buoni risultati.
La principale differenza di questo algoritmo rispetto al filtro di Kalman è che questo peso è relativamente fisso, mentre nel filtro di Kalman i pesi vengono aggiornati in modo permanente in base al rumore misurato delle letture dell'accelerometro. Il filtro di Kalman è focalizzato a darti "i migliori" risultati teorici, mentre questo algoritmo può darti risultati "abbastanza buoni" per la tua applicazione pratica. È possibile implementare un algoritmo che regoli wGyro in base ad alcuni fattori di rumore misurati, ma i valori fissi funzioneranno bene per la maggior parte delle applicazioni.
Siamo a un passo dall'ottenere i nostri valori stimati aggiornati:
RxEst(n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst(n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst(n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
Ora normalizziamo di nuovo questo vettore:
R = SQRT(RxEst(n) ^2 + RyEst(n)^2 + RzEst(n)^2)
RxEst(n) = RxEst(n)/R RyEst(n) = RyEst(n)/R RzEst(n) = RzEst(n)/R
E siamo pronti a ripetere di nuovo il nostro ciclo.
Questa guida è apparsa originariamente su starlino.com, ho apportato alcune leggere modifiche e l'ho ripubblicata con il permesso. Grazie Starlino!
Consigliato:
Accelerometro/giroscopio per controller Xbox 360 Mod: 7 passaggi

Accelerometro/giroscopio per controller Xbox 360: ho giocato ad Assetto Corsa con il mio controller Xbox 360. Sfortunatamente, lo sterzo con lo stick analogico è molto ingombrante e non ho lo spazio per una configurazione delle ruote. Ho provato a pensare a come potrei inserire un meccanismo di sterzo migliore in t
Simulatore di gioco per smartphone: gioca a giochi per Windows utilizzando il controllo gestuale IMU, accelerometro, giroscopio, magnetometro: 5 passaggi
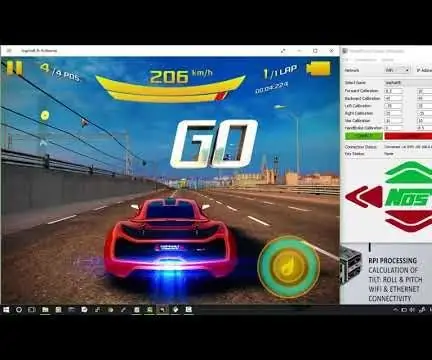
Simulatore di gioco per smartphone: gioca a giochi per Windows utilizzando il controllo gestuale IMU, accelerometro, giroscopio, magnetometro: supporta questo progetto: https://www.paypal.me/vslcreations donando a codici open-source & supporto per un ulteriore sviluppo
Arduino Nano e Visuino: convertire l'accelerazione in angolo da accelerometro e giroscopio MPU6050 Sensore I2C: 8 passaggi (con immagini)
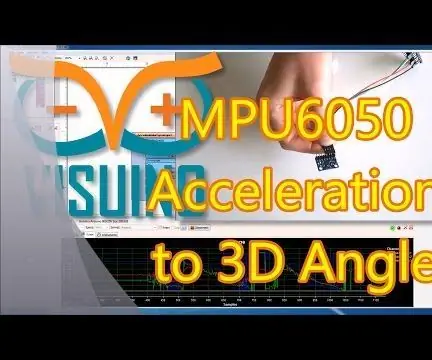
Arduino Nano e Visuino: convertire l'accelerazione in angolo da accelerometro e giroscopio MPU6050 Sensore I2C: Tempo fa ho pubblicato un tutorial su come collegare l'accelerometro, il giroscopio e il sensore bussola MPU9250 ad Arduino Nano e programmarlo con Visuino per inviare dati a pacchetto e visualizzare su un oscilloscopio e strumenti visivi. L'accelerometro invia X, Y
Arduino Nano: Accelerometro Giroscopio Bussola MPU9250 Sensore I2C con Visuino: 11 passaggi
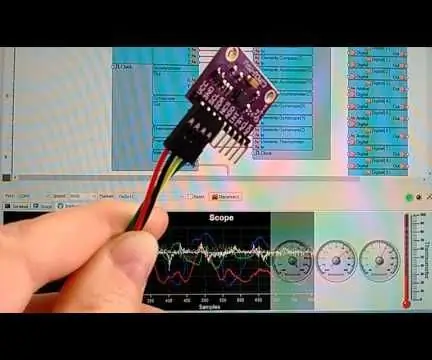
Arduino Nano: Accelerometro Giroscopio Bussola Sensore MPU9250 I2C con Visuino: MPU9250 è uno dei più avanzati sensori combinati accelerometro, giroscopio e bussola di piccole dimensioni attualmente disponibili. Hanno molte funzionalità avanzate, tra cui il filtro passa basso, il rilevamento del movimento e persino un processore specializzato programmabile
Misurazione dell'angolo con giroscopio, accelerometro e Arduino: 5 passaggi

Misurazione dell'angolo con giroscopio, accelerometro e Arduino: il dispositivo è un prototipo approssimativo di quello che alla fine diventerà un robot di autobilanciamento, questa è la seconda parte del foro (leggere l'accelerometro e controllare un motore per l'autobilanciamento). La prima parte con solo il giroscopio può essere trovata qui. Su questo is
