
Sommario:
- Autore John Day day@howwhatproduce.com.
- Public 2024-01-30 09:59.
- Ultima modifica 2025-01-23 14:49.


Ecco un'applicazione pratica di equazioni matematiche complesse.
Si tratta infatti di una tecnica molto utile che si può utilizzare per caratterizzare componenti, o anche un'antenna, a frequenze predeterminate.
Se hai armeggiato con l'elettronica, potresti avere familiarità con i resistori e la legge di Ohm. R = V / I Ora potresti essere sorpreso di sapere che questo è tutto ciò di cui hai bisogno per risolvere anche le impedenze complesse! Tutte le impedenze sono essenzialmente complesse, cioè hanno una parte Reale e una Immaginaria. Nel caso di un resistore l'immaginario (o reattanza) è 0, di conseguenza non c'è differenza di fase tra V e I, quindi possiamo lasciarli fuori.
Un rapido riassunto sui numeri complessi. Complesso significa semplicemente che il numero è composto da due parti, una reale e una immaginaria. Ci sono due modi per rappresentare numeri complessi, ad esempio nella figura sopra, un punto potrebbe essere definito dai valori Reale e Immaginario, come dove si incontrano le linee gialla e blu. Ad esempio, se la linea blu fosse a 4 sull'asse X e 3 sull'asse Y, questo numero sarebbe 4 + 3i, i indica che questa è la parte immaginaria di questo numero. Un altro modo per definire lo stesso punto sarebbe dalla lunghezza (o ampiezza) della linea rossa e dall'angolo che forma con l'orizzontale. Nell'esempio sopra questo sarebbe 5 < 36,87.
O una linea con una lunghezza di 5 con un angolo di 36,87 gradi.
Nell'equazione soprattutto dei parametri, R, V e I si può pensare che abbiano una parte immaginaria, quando si lavora con resistori questo valore è 0.
Quando si lavora con induttanze o condensatori, o quando è possibile misurare una differenza di fase (in gradi) tra i segnali, l'equazione rimane la stessa ma deve essere inclusa la parte immaginaria del numero. La maggior parte dei calcolatori scientifici rende molto facile lavorare con la matematica complessa, in questo tutorial lavorerò attraverso un esempio su un Casio fx-9750GII.
Innanzitutto, un riepilogo dell'equazione del partitore di tensione del resistore.
Come da figura -
La tensione in Y è la corrente i moltiplicata per R2
i è la tensione X divisa per la somma di R1 e R2
Quando R2 è sconosciuto, possiamo misurare gli altri valori, X, Y, R1 e riorganizzare l'equazione per risolvere R2.
Forniture
Calcolatrice scientifica
Generatore di segnale
Oscilloscopio
Passaggio 1: configurazione

Supponiamo di voler calcolare l'induttanza del Device Under Test (DUT) a 1MHz.
Il generatore di segnale è configurato per un'uscita sinusoidale di 5V a 1MHZ.
Stiamo usando resistori da 2k ohm e i canali dell'oscilloscopio sono CH1 e CH2
Passaggio 2: oscilloscopio

Otteniamo le forme d'onda come mostrato in figura. Uno sfasamento può essere visto e misurato sull'oscilloscopio in anticipo di 130 ns. L'ampiezza è 3,4V. Nota, il segnale su CH1 dovrebbe essere 2,5 V poiché viene preso all'uscita del partitore di tensione, qui è mostrato come 5 V per chiarezza, poiché questo è il valore che dobbiamo usare anche nei nostri calcoli. cioè 5V è la tensione di ingresso al divisore con il componente sconosciuto.
Passaggio 3: calcola la fase

A 1MHz il periodo del segnale in ingresso è 1us.
130ns dà un rapporto di 0,13. O 13%. Il 13% di 360 è 46,6
Al segnale 5V viene assegnato un angolo di 0.. poiché questo è il nostro segnale di ingresso e lo sfasamento è relativo ad esso.
al segnale a 3,4 V viene assegnato l'angolo di +46,6 (il + significa che è in anticipo, per un condensatore l'angolo sarebbe negativo).
Passaggio 4: sulla calcolatrice


Ora inseriamo semplicemente i nostri valori misurati nella calcolatrice.
R è 2k
V è 5 (EDIT - V è 5, più avanti nell'equazione viene utilizzato X! Il risultato è esattamente lo stesso di X come 5 nella mia calcolatrice)
Y è la nostra tensione misurata con l'angolo di fase, questo numero viene inserito come numero complesso, semplicemente specificando l'angolo come mostrato sullo schermo della calcolatrice
Passaggio 5: risolvere l'equazione

ora l'equazione
(Y * R) / (X - Y)
viene digitato nella calcolatrice, questa è esattamente la stessa equazione che usiamo per risolvere i divisori di tensione dei resistori:)
Passaggio 6: valori calcolati


La calcolatrice ha prodotto il risultato
18 + 1872i
Il 18, è la parte reale dell'impedenza ed ha un'induttanza di +1872 a 1MHz.
Che funziona a 298uH secondo l'equazione dell'impedenza dell'induttore.
18 ohm è superiore alla resistenza che verrebbe misurata con un multimetro, questo perché il multimetro misura la resistenza in CC. A 1MHz c'è l'effetto pelle, in cui la parte interna del conduttore è bypassata dalla corrente e scorre solo all'esterno del rame, diminuendo di fatto l'area d'incrocio del conduttore e aumentandone la resistenza.
Consigliato:
Il sistema di archiviazione dei componenti: 10 passaggi (con immagini)

The Component Storage System: The Ultimate Component Storage System è una soluzione unica per organizzare e conservare i componenti elettronici. Il software personalizzato consente la catalogazione dei componenti con una funzione di ricerca integrata per ottenere un rapido accesso a componenti specifici. LED su
Calcoli importanti in elettronica: 7 passaggi

Calcoli importanti in elettronica: questo Instructable intende elencare alcuni dei calcoli importanti di cui gli ingegneri/produttori elettronici devono essere a conoscenza. Francamente ci sono molte formule che possono rientrare in questa categoria. Quindi ho limitato questo Instructable alle fo
Saldatura a mano Divertente cattivo dei componenti elettronici del circuito di scarto: 7 passaggi

Saldatura a mano Funny Villain of Scrap Circuit Board Componenti elettronici: rottami di circuiti elettronici (vecchi computer o elettrodomestici di scarto) saldatore, pinzette per saldatura, pinze, forbici
Dissaldatura di componenti complessi: 4 passaggi

Dissaldatura di componenti complessi: hai mai desiderato estrarre quel chip o componente casuale da quel circuito stampato casuale che hai? Certo che è facile da fare con cose come condensatori o LED, ma quando si tratta di cose più complesse diventa un po' più difficile … E quando le cose si fanno difficili
Misurare l'impedenza usando LTspice: 4 passaggi
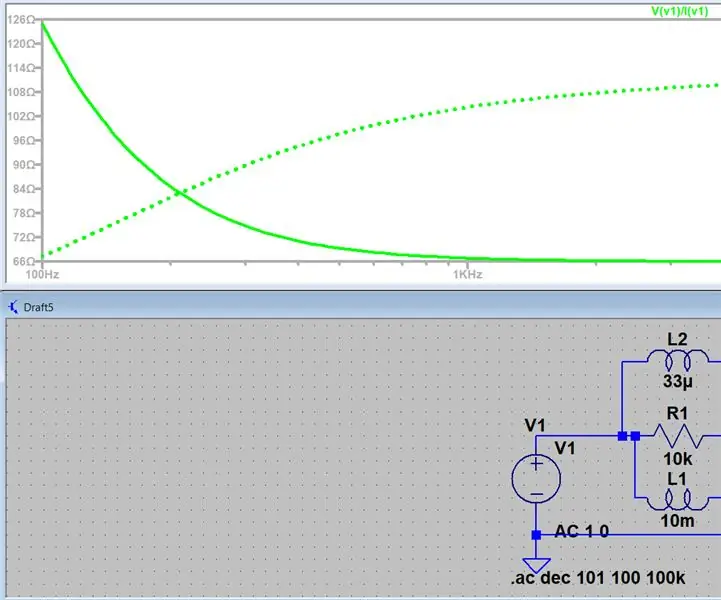
Misurare l'impedenza usando LTspice: Ciao a tutti, questa sarà una semplice introduzione alla generazione di uno sweep AC di un circuito e alla ricerca dell'impedenza in un dato punto, questo è emerso più volte nei miei corsi ed è stato molto difficile per me trovare qualsiasi modo per farlo online quindi
