
Sommario:
- Passaggio 1: leggere il seguente problema
- Passaggio 2: identificare
- Passaggio 3: utilizzare la seguente formula per trovare il "punteggio z"
- Passaggio 4: sottrarre il livello di rifiuto da "1"
- Passaggio 5: test a due code o a una coda?
- Passaggio 6: passaggio aggiuntivo per il test a due code
- Passaggio 7: utilizzare la tabella Z
- Passaggio 8: rifiutare l'ipotesi nulla o non rifiutare l'ipotesi nulla
- Passaggio 9: determinare il significato statistico
- Passaggio 10: controlla le tue risposte
- Autore John Day day@howwhatproduce.com.
- Public 2024-01-30 10:02.
- Ultima modifica 2025-06-01 06:09.

Panoramica:
Scopo: in questo tutorial imparerai come determinare se esiste una significatività statistica tra due variabili in relazione a un problema di assistenza sociale. Utilizzerai un test Z per determinare questo significato.
Durata: 10-15 minuti, 10 passi
Materiali di consumo: utensile da scrittura, carta e calcolatrice
Livello di difficoltà: sarà necessaria una conoscenza di base dell'algebra
Termini (in ordine alfabetico):
Media calcolata: la media dei valori determinata dal tester
Dimensione della popolazione: nelle statistiche, tutti gli individui, gli oggetti o gli eventi che soddisfano i criteri di studio
Ipotesi nulla - L'affermazione che non esiste alcuna relazione tra due variabili di interesse
Livello di rifiuto: livello di probabilità selezionato al quale l'ipotesi nulla viene respinta
A due code: la relazione tra le variabili va in entrambe le direzioni, il che significa che il test sta determinando se esiste una variabile che ha un effetto complessivo sull'altra variabile. Ex. Tra gli assistenti medico-sociali, le donne e gli uomini differiranno nei loro livelli di soddisfazione sul lavoro
A una coda: la relazione tra la variabile è in una direzione specifica. Ex. Le assistenti sociali mediche avranno livelli più elevati di soddisfazione sul lavoro rispetto agli assistenti sociali medici maschi
Significatività statistica - Giudicato troppo improbabile che si sia verificato a causa di un errore di campionamento
Media vera/prevista: la media originale dei valori
Vera deviazione standard: quanto varia un insieme di valori; ci consente di scoprire quanto è probabile che un valore specifico venga ottenuto eseguendo un test Z
Z-score - Una misura di quante deviazioni standard al di sotto o al di sopra della popolazione significano un punteggio è
Z-test - Una procedura di verifica delle ipotesi utilizzata per decidere se le variabili hanno significatività statistica
Z-table - Una tabella utilizzata per calcolare la significatività statistica
Passaggio 1: leggere il seguente problema
Sono interessato a studiare l'ansia tra gli studenti che studiano per le medie. So che la vera media sulla scala dell'ansia di tutti gli studenti è 4 con una deviazione standard reale di 1. Sto studiando un gruppo di 100 studenti che studiano per le medie. Calcolo una media per questi studenti su questa scala di 4.2. (Nota: punteggi più alti = maggiore ansia). Il livello di rifiuto è 0,05. C'è una differenza statisticamente significativa tra la popolazione studentesca generale e gli studenti che studiano per le medie su questa scala?
Passaggio 2: identificare
un. La vera media (media attesa)
B. La vera deviazione standard della popolazione
C. La media calcolata (media osservata)
D. La dimensione della popolazione
e. Il livello di rifiuto
Passaggio 3: utilizzare la seguente formula per trovare il "punteggio z"

z = (media osservata-media attesa)
(deviazione standard/ sizedimensione della popolazione)
Passaggio 4: sottrarre il livello di rifiuto da "1"
Scrivi questo valore
Passaggio 5: test a due code o a una coda?
Per definizioni ed esempi di test a due code e a una coda, fare riferimento all'inizio dell'istruzione alla sezione intitolata: "Termini"
Annotare se il test è a due code o a una coda.
Passaggio 6: passaggio aggiuntivo per il test a due code
Se il test è a una coda, lasciare il numero calcolato nel passaggio 3 così com'è. Se è a due code, dividi a metà il valore calcolato dal passaggio 3.
Annota questo numero.
Passaggio 7: utilizzare la tabella Z


Accedi alla tabella Z, che è la prima tabella in questo passaggio. Usando il numero che hai annotato nel passaggio 6, trovalo al centro della tabella. Una volta trovato il numero al centro, usa la colonna all'estrema sinistra e la riga in alto per determinare il valore.
Scrivi il valore. Per ulteriori istruzioni per trovare questo valore, il seguente è un esempio di come utilizzare la tabella z:
Se il tuo numero fosse "0.0438" calcolato nel passaggio 6, come si trova nella sezione trasversale della colonna 3 e della riga 3 nell'estratto della tabella z, il tuo valore sarebbe 0,11. La colonna all'estrema sinistra della tabella ha il valore della prima cifra decimale. La riga superiore ha il valore per la seconda cifra decimale. Vedere la seconda immagine di un estratto della tabella z per un esempio.
Passaggio 8: rifiutare l'ipotesi nulla o non rifiutare l'ipotesi nulla
Confronta il numero che hai trovato nel passaggio 7 con il numero che hai calcolato nella domanda 3 per determinare se devi rifiutare l'ipotesi nulla o se non devi rifiutare l'ipotesi nulla.
Annotare il numero del passaggio 3 Annotare il numero del passaggio 7
Se il numero calcolato dal passaggio 7 è inferiore al numero calcolato al passaggio 3, devi rifiutare l'ipotesi nulla. Se il numero calcolato dal passaggio 7 è maggiore del numero calcolato al passaggio 3, non si rifiuta l'ipotesi nulla
Rifiutare l'ipotesi nulla o non rifiutare l'ipotesi nulla?
Passaggio 9: determinare il significato statistico
Se rifiuti l'ipotesi nulla, allora c'è una significatività statistica tra le variabili. Se non si rifiuta l'ipotesi nulla, non c'è una significatività statistica tra le variabili.
Annotare se c'è o se non c'è una significatività statistica
Passaggio 10: controlla le tue risposte
- Passaggio 3: 2
- Passaggio 5: a due code
- Passaggio 6: 0,475
- Passaggio 7: 1,96
- Passaggio 8: poiché 1.96 < 2, devi rifiutare l'ipotesi nulla
- Passaggio 9: esiste una significatività statistica
Consigliato:
Controllore automatico della luce e della ventola della stanza con contatore visitatori bidirezionale: 3 passaggi

Controllore automatico della luce e della ventola della stanza con contatore visitatori bidirezionale: spesso vediamo contatori visitatori in stadi, centri commerciali, uffici, aule, ecc. Come contano le persone e accendono o spengono la luce quando nessuno è all'interno? Oggi siamo qui con il progetto di controllo automatico della luce ambientale con contatore visitatori bidirezionale
Hackerare un pulsante della porta della Jubilee Line della metropolitana di Londra: 12 passaggi (con immagini)

Hacking di un pulsante della porta della Jubilee Line della metropolitana di Londra: Il negozio del London Transport Museum vende pulsanti della porta dismessi della Jubilee Line (sono disponibili sia a sinistra che a destra). Se stai pensando di realizzare un progetto che necessita di un pulsante e di una spia di qualche tipo, saresti
ESP8266 Nodemcu Monitoraggio della temperatura utilizzando DHT11 su un server Web locale - Ottieni la temperatura e l'umidità della stanza sul tuo browser: 6 passaggi
ESP8266 Nodemcu Monitoraggio della temperatura utilizzando DHT11 su un server Web locale | Ottieni la temperatura e l'umidità della stanza sul tuo browser: Ciao ragazzi, oggi faremo un'umidità e l'umidità; sistema di monitoraggio della temperatura utilizzando ESP 8266 NODEMCU & Sensore di temperatura DHT11. La temperatura e l'umidità saranno ottenute da DHT11 Sensor & può essere visto su un browser quale pagina web verrà gestita
Visualizzazione della pressione barometrica e della temperatura utilizzando Infineon XMC4700 RelaxKit, Infineon DPS422 e AWS.: 8 passaggi
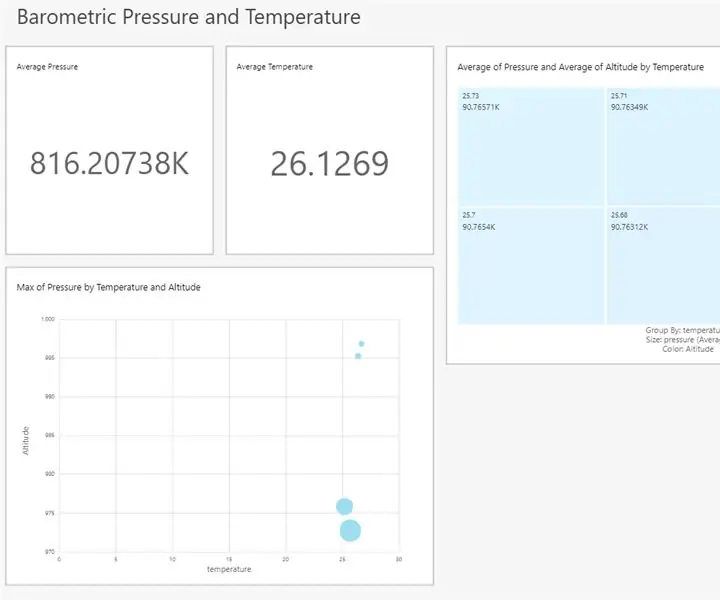
Visualizzazione della pressione atmosferica e della temperatura utilizzando Infineon XMC4700 RelaxKit, Infineon DPS422 e AWS.: È un progetto semplice per acquisire la pressione atmosferica e la temperatura utilizzando il DPS 422 di Infineon. Diventa goffo monitorare la pressione e la temperatura per un periodo di tempo. È qui che entra in gioco l'analisi, l'intuizione sul cambiamento in
Determinazione della pressione e dell'altitudine utilizzando GY-68 BMP180 e Arduino: 6 passaggi

Determinazione della pressione e dell'altitudine utilizzando GY-68 BMP180 e Arduino: PanoramicaIn molti progetti come robot volanti, stazioni meteorologiche, miglioramento delle prestazioni di routing, sport e così via, la misurazione della pressione e dell'altitudine è molto importante. In questo tutorial imparerai come utilizzare il sensore BMP180, che è uno dei più
